Question

simply supported beam is subjected to a linearly varying distributed load ( ) 0 q x x L 5 q with maximum intensity 0 q at B. The beam has a length L 5 4 m and rectangular cross section with a width of 200 mm and height of 300 mm. Determine the maximum permissible value for the maximum inten- sity, 0 q , if the allowable normal stresses in tension and compression are 120 MPa.

Answer 1

q₀ = 350,740.2885 N/m

Step-by-step explanation:

Given

`q(x)=(x)/(L) q_(0)`

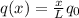
σ = 120 MPa = 120*10⁶ Pa

`L=4 m\\w=200 mm=0.2m\\h=300 mm=0.3m\\q_(0)=? \\`

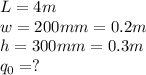
We can see the pic shown in order to understand the question.

We apply

∑MB = 0 (Counterclockwise is the positive rotation direction)

⇒ - Av*L + (q₀*L/2)*(L/3) = 0

⇒ Av = q₀*L/6 (↑)

Then, we apply

`v(x)=\int\limits^L_0 {q(x)} \, dx\\v(x)=-(q_(0))/(2L) x^(2)+(q_(0) L)/(6) \\M(x)=\int\limits^L_0 {v(x)} \, dx=-(q_(0))/(6L) x^(3)+(q_(0) L)/(6)x`

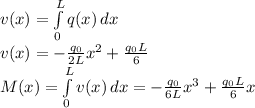
Then, we can get the maximum bending moment as follows

`M'(x)=0\\ (-(q_(0))/(6L) x^(3)+(q_(0) L)/(6)x)'=0\\ -(q_(0))/(2L) x^(2)+(q_(0) L)/(6)=0\\x^(2) =(L^(2))/(3)\\ x=\sqrt{(L^(2))/(3)} =(L)/(√(3) )=(4)/(√(3) )m`

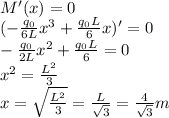
then we get

`M((4)/(√(3) ))=-(q_(0))/(6*4) ((4)/(√(3) ))^(3)+(q_(0) *4)/(6)((4)/(√(3) ))\\ M((4)/(√(3) ))=-(8)/(9√(3) ) q_(0) +(8)/(3√(3) ) q_(0)=(16)/(9√(3) ) q_(0)m^(2)`

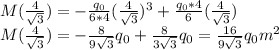
We get the inertia as follows

`I=(w*h^(3) )/(12) \\ I=(0.2m*(0.3m)^(3) )/(12)=4.5*10^(-4)m^(4)`

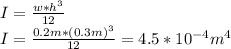
We use the formula

σ = M*y/I

⇒ M = σ*I/y

where

`y=(h)/(2) =(0.3m)/(2)=0.15m`

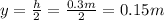
If M = Mmax, we have

`((16)/(9√(3) )m^(2) ) q_(0)\leq (120*10^(6)Pa*4.5*10^(-4)m^(4) )/(0.15m)\\ q_(0)\leq 350,740.2885(N)/(m)`