Answer:
30,000 units
Step-by-step explanation:
According to the inventory cost model, the production run size that minimizes costs is given by:
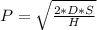
Where D is the annual demand (1,500,000 items), S is the cost of each production run ($900) and H is the holding cost per unit ($3). Applying the given data:
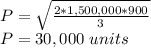
Each production run should consist of 30,000 units.