Question

Suppose you are going to conduct a two tail test concerning the population mean. Suppose that you do not know what the population standard deviation is and that you have a sample of 55 observations. If you are going to conduct this test at the .01 level of significance what is the critical value?

Answer 1

The critical value of t at 0.01 level of significance is 2.66.

Explanation:

The hypothesis for the two-tailed population mean can be defined as:

H₀: μ = μ₀ vs. H₀: μ ≠ μ₀

It is provided that the population standard deviation is not known.

Since there is no information about the population standard deviation, we will use a t-test for single mean.

The test statistic is defined as follows:

`t_(cal.)=(\bar x-\mu)/(s/√(n))\sim t_(\alpha/2, (n-1))`

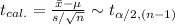
The information given is:

n = 55

α = 0.01

Compute the critical value of t as follows:

`t_(\alpha/2, (n-1))= t_(0.01/2, (55-1))=t_(0.005, 54)=2.66`

*Use a t-table for the value.

If the desired degrees of freedom are not provided consider he next highest degree of freedom.

Thus, the critical value of t at 0.01 level of significance is 2.66.