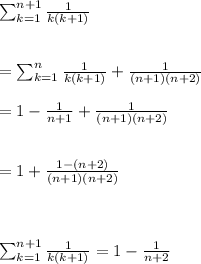Question

Proof: let LaTeX: P\left(n\right)=\sum_{k=1}^n\frac{1}{k(k+1)}=1-\frac{1}{n+1}.P ( n ) = ∑ k = 1 n 1 k ( k + 1 ) = 1 − 1 n + 1 . Base case: P(1) = 1/2. Inductive step: suppose P(n) has already been proven for some arbitrary n. The statement P(n+1) is LaTeX: P\left(n+1\right)=\sum_{k=1}^{n+1}\frac{1}{k\left(k+1\right)}=1-\frac{1}{n+2}P ( n + 1 ) = ∑ k = 1 n + 1 1 k ( k + 1 ) = 1 − 1 n + 2 This concludes the proof by induction.

Answer 1

`\\\sum_(k=1)^(n+1)(1)/(k(k+1))\\ \\ \\=\sum_(k=1)^n(1)/(k(k+1))+(1)/((n+1)(n+2)) \\ \\ =1-(1)/(n+1)+(1)/((n+1)(n+2))\\ \\ \\ =1+(1-(n+2))/((n+1)(n+2)) \\ \\ \\ \\\sum_(k=1)^(n+1)(1)/(k(k+1)) =1-(1)/(n+2)`

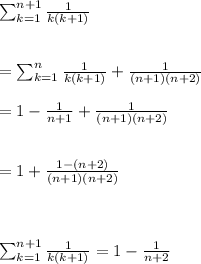
Explanation:

The question says; Proof that :

`Let : P\left(n\right)=\sum_(k=1)^n(1)/(k(k+1))=1-(1)/(n+1)`

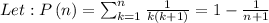
Base case: P(1) = 1/2.

Inductive step: suppose P(n) has already been proven for some arbitrary n. The statement P(n+1) is :

`P\left(n+1\right)=\sum_(k=1)^(n+1)(1)/(k\left(k+1\right))=1-(1)/(n+2)`

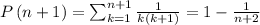
This concludes the proof by induction.

We Proof that:

The proof abuses the notation P(n) to make reference to the common values of the two sides of the equation to be proved. Moreover, it doesn't makes any sense to define P(n) as the common value of the two sides because it assumes the conclusion that the two sides are equal.

At the very least, the definition of P(n) in the first statement suppose to have be in quote or in parenthesis as shown below.

`Let : P\left(n\right)=(\sum_(k=1)^n(1)/(k(k+1))=1-(1)/(n+1))`

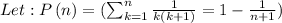
However , P(n) is a statement.

The proof writer confused stating P(n+1) with showing that it must be true; given that P(n) is true.

As such ; the correct proof for P(n+1) is:

`\\\sum_(k=1)^(n+1)(1)/(k(k+1))\\ \\ \\=\sum_(k=1)^n(1)/(k(k+1))+(1)/((n+1)(n+2)) \\ \\ =1-(1)/(n+1)+(1)/((n+1)(n+2))\\ \\ \\ =1+(1-(n+2))/((n+1)(n+2)) \\ \\ \\ \\\sum_(k=1)^(n+1)(1)/(k(k+1)) =1-(1)/(n+2)`