Question

An electron is accelerated from rest by a potential difference of 412 V. It then enters a uniform magnetic field of magnitude 188 mT with its velocity perpendicular to the field. Calculate (a) the speed of the electron and (b) the radius of its path in the magnetic field.

Answer 1

Step-by-step explanation:

Given that,

Potential difference, V = 412 V

Magnitude of magnetic field, B = 188 mT

(a) The potential energy of electron is balanced by its kinetic energy as :

`eV=(1)/(2)mv^2`

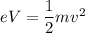
v is speed of the electron

`v=\sqrt{(2eV)/(m)} \\\\v=\sqrt{(2* 1.6* 10^(-19)* 412)/(9.1* 10^(-31))} \\\\v=1.2* 10^7\ m/s`

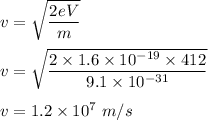
(b) When the charged particle moves in magnetic field, it will move in circular path. The radius of the circular path is given by :

`r=(mv)/(eB)\\\\r=(9.1* 10^(-31)* 1.2* 10^7)/(1.6* 10^(-19)* 188* 10^(-3))\\\\r=3.63* 10^(-4)\ m`

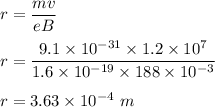
Hence, this is the required solution.