Question

Not in Book 4 : 4 kooB nI toN [2 points] A palindrome is a string that’s the same forward as it is backwards. Examples include "a", "racecar", "hannah", "rats live on no evil star", "" The algorithm below takes in a string and returns the length of the longest prefix of the string that’s a palindrome. Example input-output pairs include ("apple", 1), ("attack", 4), ("racecar", 7)

Answer 1

Θn²

Completed question below:

A palindrome is a string that's the same forward as it is backwards. Examples include "a”, “racecar”, “hannah”, “rats live on no evil star”, “ The algorithm below takes in a string and returns the length of the longest prefix of the string that's a palindrome. Example input-output pairs include (“apple”, 1), (“attack”, 4), (“racecar”, 7).

Find a tight bound (O) on the runtime (number of steps) of the following algorithm:

palindrome-prefix (s)

1. n <---length (s)

2. current_best to

3. for i <--- 1 to n

4. is-palindrome + true

5. for j <--- 1 to i :

6. if s[j] = s[i+1-j] then

7. is_palindrome <--- False

8. if is_palindrome then

9. current_best <---i

10. return current_best

Note: s[i] means the ith character from string s.

Step-by-step explanation:

The outer loop iterates i values from 1 to n and for each of those outer iterations, inner loop iterates i times.

Total iterations = 1 +2 + 3 + 4.....+ n =
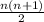`(n(n+1))/(2)` which is the sum of the series

`(n(n+1))/(2)` =
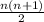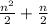`(n^(2) )/(2) + (n)/(2)` = 0.5 n² + 0.5 n.

Therefore, the time complexity is Θn²