Question

An automobile traveling 92.0 km/h has tires of 64.0 cm diameter. (a) What is the angular speed of the tires about their axles? (b) If the car is brought to a stop uniformly in 38.0 complete turns of the tires, what is the magnitude of the angular acceleration of the wheels? (c) How far does the car move during the braking? (Note: automobile moves without sliding)

Answer 1

76.4035 m

Step-by-step explanation:

r = Radius = 0.32 m

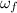`\omega_f` = Final angular velocity = 0

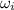`\omega_i` = Initial angular velocity = 92 km/h

`\alpha` = Angular acceleration

`\theta` = Angle of rotation

Angular speed is given by

`\omega=(v)/(r)\\\Rightarrow \omega=((92)/(3.6))/(0.32)\\\Rightarrow \omega=79.861\ rad/s`

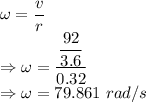
The angular speed of the tires about their axles is 79.861 rad/s.

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \alpha=(\omega_f^2-\omega_i^2)/(2\theta)\\\Rightarrow \alpha=(0^2-79.861^2)/(2* 2\pi * 38)\\\Rightarrow \alpha=-13.355\ rad/s^2`

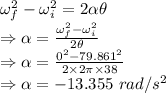
The magnitude of acceleration is 13.355 m/s²

Distance is given by

`d=\theta r\\\Rightarrow d=38* 2\pi* 0.32\\\Rightarrow d=76.4035\ m`

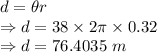
The distance moved while slowing down is 76.4035 m