Question

Use this information to answer the following 6 questions: A study is being conducted to compare the average training time for two groups of airport security personnel: those who work for the federal government and those employed by private security companies. From a random sample of 12 government-employed security personnel, average training time was 72 hours, with a sample standard deviation of 8 hours. In a random sample of 16 privately employed security personnel, training time was 65.4 hours, with a sample standard deviation of 12.3 hours. Assume that training time for each group is normally distributed. Use the following notations: μ1: The mean training time for the population of airport security personnel employed by the federal government. μ2: The mean training time for the population of airport security personnel employed by private security companies. The goal of the statistical analysis is to determine whether the sample data support the hypothesis that average training time for government-employed security personnel is higher than those employed by private security companies.

Answer 1

We conclude that the average training time for government-employed security personnel is lesser than or equal to those employed by private security companies.

Explanation:

We are given that a random sample of 12 government-employed security personnel, average training time was 72 hours, with a sample standard deviation of 8 hours. In a random sample of 16 privately employed security personnel, training time was 65.4 hours, with a sample standard deviation of 12.3 hours.

We have to conduct a hypothesis test to determine that average training time for government-employed security personnel is higher than those employed by private security companies.

Let
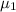`\mu_1` = mean training time for the population of airport security personnel employed by the federal government.

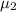`\mu_2` = mean training time for the population of airport security personnel employed by private security companies.

SO, Null Hypothesis,
`H_0` :
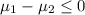`\mu_1-\mu_2\leq0` or
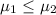`\mu_1\leq \mu_2` {means that the average training time for government-employed security personnel is lesser than or equal to those employed by private security companies}

Alternate Hypothesis,
`H_A` :
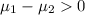`\mu_1-\mu_2>0` or
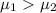`\mu_1>\mu_2` {means that the average training time for government-employed security personnel is higher than those employed by private security companies}

The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n__1+_n__2-2`

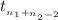
where,
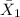`\bar X_1` = sample average training time of government-employed security personnel = 72 hours

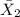`\bar X_2` = sample average training time of privately employed security personnel = 65.4 hours

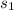`s_1` = sample standard deviation of government-employed security personnel = 8 hours

`s_2` = sample standard deviation of privately employed security personnel = 12.3 hours

`n_1` = sample of government-employed security personnel = 12

`n_2` = sample of privately employed security personnel = 16

Also,
`s_p=\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
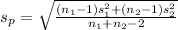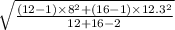`\sqrt{((12-1)* 8^(2)+(16-1)* 12.3^(2) )/(12+16-2) }` = 10.694

So, test statistics =
`\frac{(72-65.4)-(0)}{10.694 * \sqrt{(1)/(12)+(1)/(16) } }` ~
`t_2_6`

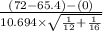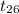
= 1.616

Since, in the question we are not given with the level of significance at which hypothesis can be tested, so we assume it to be 5%. Now at 5% significance level, the t table gives critical value of 1.706 at 26 degree of freedom for right-tailed test. Since our test statistics is less than the critical value of t as 1.616 < 1.706, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the average training time for government-employed security personnel is lesser than or equal to those employed by private security companies.