Question

Large sample inference: Let the test statistic,Z, have a normal distribution whenH0:μ=μ0istrue. Give as much information as you can about the p-value for each of the following situations:(a)Ha:μ > μ0, andZ= 2.0(b)Ha:μ < μ0, andZ=−2.4(c)Ha:μ6=μ0, andZ=−1.6(d)Ha:μ < μ0, andZ=−0.4.(e)Ha:μ < μ0andZ=−3.16(f)Ha:μ > μ0, andZ= 5.0(g)Ha:μ6=μ0, andZ= 2.8

Answer 1

The p-values are:

(a) p-value = 0.023 (e) p-value = 0.001

(b) p-value = 0.008 (f) p-value = 0

(c) p-value = 0.1096 (g) p-value = 0.005

(d) p-value = 0.3446

Explanation:

The p-value is well-defined as per the probability, [under the null-hypothesis (H₀)], of attaining a result equivalent to or greater than what was truly observed.

(a)

The alternate hypothesis is:

Hₐ: μ > μ₀

The test statistic value is, Z = 2.0.

Compute the p-value as follows:

`p-value=P(Z>2.0)\\=1-P(Z<2.0)\\=1-0.9773\\=0.0227\\\approx0.023`

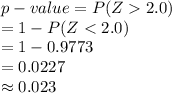
*Use a z-table.

The p-value of 0.023 implies that the probability of getting the mean value greater than or equal to μ₀ is 0.023.

(b)

The alternate hypothesis is:

Hₐ: μ < μ₀

The test statistic value is, Z = -2.4.

Compute the p-value as follows:

`p-value=P(Z<-2.4)\\=1-P(Z<2.4)\\=1-0.9918\\=0.0082\\\approx0.008`

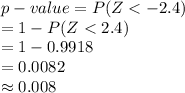
*Use a z-table.

The p-value of 0.008 implies that the probability of getting the mean value as extreme as μ₀ is 0.008.

(c)

The alternate hypothesis is:

Hₐ: μ ≠ μ₀

The test statistic value is, Z = -1.6.

Compute the p-value as follows:

`p-value=2P(Z>-1.6)\\=2[1-P(Z<1.6)]\\=2[1-0.9452]\\=0.1096`

*Use a z-table.

The p-value of 0.1096 implies that the probability of getting the mean value as extreme as μ₀ is 0.1096.

(d)

The alternate hypothesis is:

Hₐ: μ < μ₀

The test statistic value is, Z = -0.4.

Compute the p-value as follows:

`p-value=P(Z<-0.4)\\=1-P(Z<0.4)\\=1-0.65542\\=0.34458\\\approx0.3446`

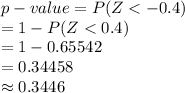
*Use a z-table.

The p-value of 0.3446 implies that the probability of getting the mean value as extreme as μ₀ is 0.3446.

(e)

The alternate hypothesis is:

Hₐ: μ < μ₀

The test statistic value is, Z = -3.16.

Compute the p-value as follows:

`p-value=P(Z<-3.16)\\=1-P(Z<3.16)\\=1-0.99921\\=0.00079\\\approx0.001`

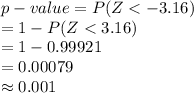
*Use a z-table.

The p-value of 0.001 implies that the probability of getting the mean value as extreme as μ₀ is 0.001.

(f)

The alternate hypothesis is:

Hₐ: μ > μ₀

The test statistic value is, Z = 5.0.

Compute the p-value as follows:

`p-value=P(Z>5.0)\\=1-P(Z<5.0)\\=1-(\approx1)\\=0`

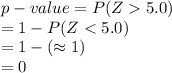
*Use a z-table.

The p-value of 0 implies that the probability of getting the mean value as extreme as μ₀ is 0.

(g)

The alternate hypothesis is:

Hₐ: μ ≠ μ₀

The test statistic value is, Z = 2.8.

Compute the p-value as follows:

`p-value=2P(Z>2.8)\\=2[1-P(Z<2.8)]\\=2[1-0.99744]\\=0.00512\\\approx0.005`

*Use a z-table.

The p-value of 0.005 implies that the probability of getting the mean value as extreme as μ₀ is 0.005.