Question

Suppose that 30% of the applicants for a certain industrial job possess advanced training in computer programming. Applicants are interviewed sequentially and are selected at random from the pool. Find the probability that the first applicant with advanced training in programming is found on the fifth interview

Answer 1

Probability that the first applicant with advanced training in programming is found on the fifth interview is 0.07203.

Explanation:

We are given that 30% of the applicants for a certain industrial job possess advanced training in computer programming.

Applicants are interviewed sequentially and are selected at random from the pool.

The above situation can be represented through geometric distribution because Geometric distribution probability gives us the probability of 1st success in
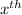`x^(th)` trial.

Since, here we want our first success in the fifth trial, i.e. the first applicant with advanced training in programming is found on the fifth interview.

The probability distribution for geometric distribution is given by;

`P(X =x) = p * (1-p)^(x-1) ; x = 1,2,3,4,......`

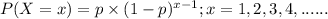
where, p = probability of success which in our question is applicant with advanced training in programming = 30%

x = no. of trials = 5

Let X = No. of applicants for a certain industrial job possess advanced training in computer programming

So, X ~ Geo( p = 0.30)

Now, probability that the first applicant with advanced training in programming is found on the fifth interview is given by = P(X = 5)

P(X = 5) =
`0.30 * (1-0.30)^(5-1)`

=
`0.30 * 0.70^(4)`

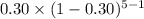
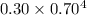
= 0.07203