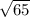Answer:
The answer to your question is
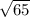
Explanation:
Data
Point A = (-9, -6)
Point B = (-2, -2)
Process
To solve this problem, substitute the values in the equation.
Formula
dAB =
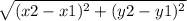
- Identify the values of x1, x2, y1 and y2
x1 = -9 y1 = -6 x2 = -2 y2 = -2
-Substitution
dAB =
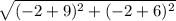
-Simplification
dAB =
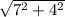
dAB =
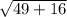
dAB =