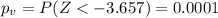Question

In a random sample of n1 = 156 male Statistics students, there are x1 = 81 underclassmen. In a random sample of n2 = 320 female Statistics students, there are x2 = 221 underclassmen. The researcher would like to test the hypothesis that the percent of males who are underclassmen stats students is less than the percent of females who are underclassmen stats students. What is the p-value for the test of hypothesis? i.e. Find P(Z < test statistic). Enter your answer to 4 decimal places.

Answer 1

`z=\frac{0.519-0.691}{\sqrt{0.634(1-0.634)((1)/(156)+(1)/(320))}}=-3.657`

`p_v =P(Z<-3.657)=0.0001`

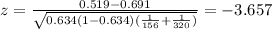
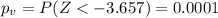
Explanation:

Data given and notation

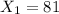`X_(1)=81` represent the number of males underclassmen

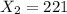`X_(2)=221` represent the number of females underclassmen

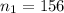`n_(1)=156` sample of male

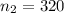`n_(2)=320` sample of female

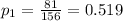`p_(1)=(81)/(156)=0.519` represent the proportion of males underclassmen

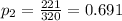`p_(2)=(221)/(320)= 0.691` represent the proportion of females underclassmen

z would represent the statistic (variable of interest)

`p_v` represent the value for the test (variable of interest)

Concepts and formulas to use

We need to conduct a hypothesis in order to check if the percent of males who are underclassmen stats students is less than the percent of females who are underclassmen stats students , the system of hypothesis would be:

Null hypothesis:
`p_(1) \geq p_(2)`

Alternative hypothesis:
`p_(1) < p_(2)`

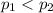
We need to apply a z test to compare proportions, and the statistic is given by:

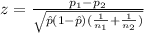`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(81+221)/(156+320)=0.634`

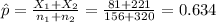
Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.519-0.691}{\sqrt{0.634(1-0.634)((1)/(156)+(1)/(320))}}=-3.657`

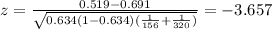
Statistical decision

For this case we don't have a significance level provided
`\alpha`, but we can calculate the p value for this test.

Since is a one side test the p value would be:

`p_v =P(Z<-3.657)=0.0001`

Answer 2

The p-value for the test of hypothesis is P(z<-3.617)=0.0002.

Explanation:

Hypothesis test on the difference between proportions.

The claim is that the percent of males who are underclassmen stats students (π1) is less than the percent of females who are underclassmen stats students (π2).

Then, the null and alternative hypothesis are:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2<0`

The male sample has a size n1=156. The sample proportion is p1=81/156=0.52.

The female sample has a size n2=221. The sample proportion in this case is p2=221/320=0.69.

The weigthed average of proportions p, needed to calculate the standard error, is:

`p=(n_1p_1+n_2p_2)/(n_1+n_2)=(81+221)/(156+320)=(302)/(476)= 0.63`

The standard error for the difference in proportions is:

`\sigma_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.63*0.37)/(156)+(0.63*0.37)/(320)}\\\\\\\sigma_(p1-p2)=\sqrt{(0.2331)/(156)+(0.2331)/(320)}=√(0.001503871+0.000728438)=√(0.002232308)\\\\\\\sigma_(p1-p2)=0.047`

Then, we can calculate the z-statistic as:

`z=(p_1-p_2)/(\sigma_(p1-p2))=(0.52-0.69)/(0.047)=(-0.17)/(0.047)=-3.617`

The P-value for this left tailed test is:

`P-value = P(z<-3.617)=0.00015`