Answer:
(a) Displacement = - 3.0576 m
(b) Velocity
 m/s
m/s
(c)Acceleration = -753.39 m²/s
(d)The phase motion is 26.7
 .
.
(e)Frequency =2.5 Hz.
(f)Time period =0.4 s
Step-by-step explanation:
Given function is
![x= (5.2 m)cos[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/xkhk712j372t2dohhz1ojrs4incfxvgso4.png)
(a)
The displacement includes the parameter t, so,at time t=5.3 s
![x|_(t=5.3)= (5.2 m)cos[ (5\pi \ rad/s)5.3+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/bo03l0tntd7w0wuq7i2ryp8ljn210jmmy5.png)
![= (5.2 m)cos[ 26.5\pi+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/d53kmsphendyjjl44wq72ug87f3abnhbsj.png)
=(5.2)(-0.588)m
= - 3.0576 m
(b)
![x= (5.2 m)cos[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/xkhk712j372t2dohhz1ojrs4incfxvgso4.png)
To find the velocity of simple harmonic motion, we need to find out the first order derivative of the function.
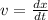
![=(d)/(dt) (5.2 m)cos[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/vd74p5t77bs2k6rjrinip98x5wzjyvkr4g.png)
![= (5.2 m)(-5\pi)sin[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/8cm1rnytqz46s6vbrwltzkjh0cr8hgfe1c.png)
![= -26\pi sin[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/qbpwoxiys01nit9saz013dlsvans6bgja2.png)
Now we can plug our value t=5.3 into the above equation
![v= -26\pi sin[ (5\pi \ rad/s)5.3\ s+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/7n4z5jpuxjmvz0pxg2wgoxrh65gdt8a4y8.png)
 m/s
m/s
(c)
To find the acceleration of simple harmonic motion, we need to find out the second order derivative of the function.
![v= -26\pi sin[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/uz4w8qfkh314pbxgxj77rb44h2dqrtuib7.png)
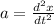
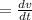
![=(d)/(dt)( -26\pi sin[ (5\pi \ rad/s)t+ \frac\pi5])](https://img.qammunity.org/2021/formulas/physics/high-school/s56cf0shxt66sw20px7t90xjt7sfaiorun.png)
![= -26\pi (5\pi)cos[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/xp7f5ao8l7najx565kops6e2wmfa7ct6tz.png)
![= -130\pi^2cos[ (5\pi \ rad/s)t+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/5zxpkx5p6c1wgzyqyppup6b40tpvv7ryap.png)
Now we can plug our value t=5.3 into the above equation
![a= -130\pi^2cos[ (5\pi \ rad/s)5.3 \ s+ \frac\pi5]](https://img.qammunity.org/2021/formulas/physics/high-school/p4xhhfy4p9305b8rjm312hahjp7b50ea6k.png)
= -753.39 m²/s
(d)
The general equation of SHM is
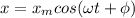
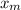 is amplitude of the displacement,
is amplitude of the displacement,
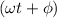 is phase of motion,
is phase of motion,
 is phase constant.
is phase constant.
So,
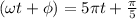
Now plugging t=5.3s
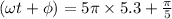
=26.7

The phase motion is 26.7
 .
.
The angular frequency
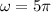
(e)
The relation between angular frequency and frequency is
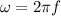
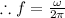
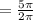
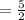
= 2.5 Hz
Frequency =2.5 Hz.
(f)
The relation between frequency and time period is
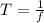
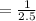
=0.4 s
Time period =0.4 s