Answer:
The sample size n= 2500
A survey with 2500 left-handed people guarantees the given margin error is 2%
Explanation:
Explanation:-
The margin of error =
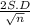
here for proportions , the standard deviation (σ) =
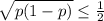
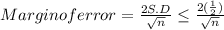
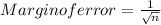
now The necessary sample size is
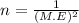
Given data the survey in order to get a margin of error of 2%
M.E = 0.02
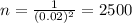
Conclusion:-
The sample size n= 2500
A survey with 2500 left-handed people guarantees the given margin error is 2%