Question

What if you wanted a smaller margin of error in your interval for the proportion of left-handed people (say plus or minus 2%)? How many people would you need to survey in order to get a margin of error of 2% ? You can use the LaTeX: \hat{p} p ^ that you already calculated as your estimate in the sample size formula.

Answer 1

The sample size n= 2500

A survey with 2500 left-handed people guarantees the given margin error is 2%

Explanation:

Explanation:-

The margin of error =
`(2 S.D)/(√(n) )`

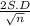
here for proportions , the standard deviation (σ) =
`√(p(1-p)) \leq (1)/(2)`

`Margin of error = (2 S.D)/(√(n) ) \leq (2((1)/(2)) )/(√(n) )`

`Margin of error = (1)/(√(n) )`

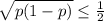
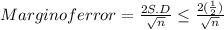
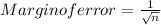
now The necessary sample size is

`n= (1)/((M.E)^(2) )`

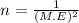
Given data the survey in order to get a margin of error of 2%

M.E = 0.02

`n= (1)/((0.02)^(2) ) = 2500`

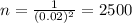
Conclusion:-

The sample size n= 2500

A survey with 2500 left-handed people guarantees the given margin error is 2%