Question

survey on televisions requiring repairs within four years was conducted. Nineteen out of 200 televisions from company A and 25 out of 200 televisions from company B needed repairs. Do these data show that televisions from company A are more reliable than televisions from company B?

Answer 1

`z=\frac{0.095-0.125}{\sqrt{0.11(1-0.11)((1)/(200)+(1)/(200))}}=-0.959`

`p_v =P(Z<-0.959)=0.169`

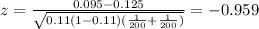
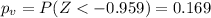
Comparing the p value with the significance level assumed
`\alpha=0.05` we see that
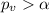`p_v>\alpha` so we can conclude that we have enough evidence to to FAIL to reject the null hypothesis, and we can't conclude that company A are more reliable than televisions from company B at 5% of significance.

Explanation:

Data given and notation

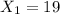`X_(1)=19` represent the number of tvs who need a repair for A

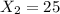`X_(2)=25` represent the number of tvs who need a repair for B

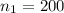`n_(1)=200` sample 1 selected

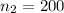`n_(2)=200` sample 2 selected

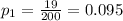`p_(1)=(19)/(200)=0.095` represent the proportion estimated for the sample A

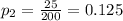`p_(2)=(25)/(200)=0.125` represent the proportion estimated for the sample B

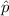`\hat p` represent the pooled estimate of p

z would represent the statistic (variable of interest)

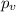`p_v` represent the value for the test (variable of interest)

`\alpha=0.05` significance level given

Concepts and formulas to use

We need to conduct a hypothesis in order to check if company A are more reliable than televisions from company B (that means p1<p2) , the system of hypothesis would be:

Null hypothesis:
`p_(1) \geq p_(2)`

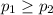
Alternative hypothesis:
`p_(1) < p_(2)`

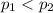
We need to apply a z test to compare proportions, and the statistic is given by:

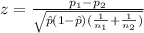`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(19+25)/(200+200)=0.11`

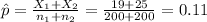
z-test: Is used to compare group means. Is one of the most common tests and is used to determine whether the means of two groups are equal to each other.

Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.095-0.125}{\sqrt{0.11(1-0.11)((1)/(200)+(1)/(200))}}=-0.959`

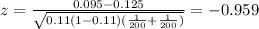
Statistical decision

Since is a left sided test the p value would be:

`p_v =P(Z<-0.959)=0.169`

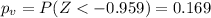
Comparing the p value with the significance level assumed
`\alpha=0.05` we see that
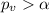`p_v>\alpha` so we can conclude that we have enough evidence to to FAIL to reject the null hypothesis, and we can't conclude that company A are more reliable than televisions from company B at 5% of significance.