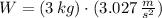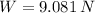Answer:
Step-by-step explanation:
The angular frequency of a simple pendulum is:
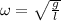
Where:
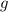 - Gravitational constant, in
- Gravitational constant, in
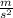 .
.
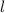 - The rod length, in m.
- The rod length, in m.
The period of oscillation of the simple pendulum is:
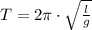
Given that the same pendulum is tested of both planets, the following relation is determined:
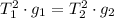
The gravity constant on Planet X is:
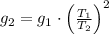
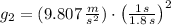
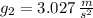
The weight of the pendulum bob on Planet X is: