The horizontal asymptote is at y=4, shown by the green dashed line. This indicates the behavior of the function as x becomes very large in magnitude.
The blue dot marks the y-intercept at (0,6).
To find the graph that represents the function
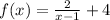 , let's analyze its characteristics step by step:
, let's analyze its characteristics step by step:
1. Identify the Type of Function
The function
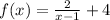 is a rational function, specifically a transformed version of the reciprocal function.
is a rational function, specifically a transformed version of the reciprocal function.
2. Vertical Asymptote
The denominator
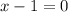 gives the vertical asymptote, which is
gives the vertical asymptote, which is
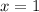 . This means the graph will approach but never touch the line
. This means the graph will approach but never touch the line
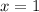 .
.
3. Horizontal Asymptote
For large values of x, the term
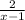 approaches zero. Thus, the horizontal asymptote is determined by the constant term, which is
approaches zero. Thus, the horizontal asymptote is determined by the constant term, which is
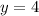 .
.
4. Y-Intercept
To find the y-intercept, set
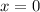 :
:
![\[ f(0) = (2)/(0-1) + 4 = 2 + 4 = 6 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/crj6fvztz8p5w3x0sagax2ml7m5nb691ue.png)
So, the y-intercept is at (0, 6).
5. Behavior around Asymptotes
- As x approaches 1 from the left,
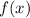 goes to negative infinity.
goes to negative infinity. - As x approaches 1 from the right,
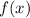 goes to positive infinity.
goes to positive infinity.
6. Additional Points
It might be helpful to calculate the function's value at a couple of additional points for a more accurate graph. For instance, calculate
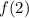 and
and
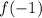 .
.
7. Sketching the Graph
Considering these characteristics, the graph:
- Has a vertical asymptote at
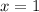 .
. - Has a horizontal asymptote at
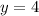 .
. - Passes through the y-intercept at (0, 6).
- Shows the function going to negative infinity as x approaches 1 from the left and to positive infinity as x approaches 1 from the right.
Here is the graph of the function
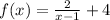 . As analyzed:
. As analyzed:
(Graph is give below)
It has a vertical asymptote at x=1, represented by the red dashed line. The function goes to negative infinity as x approaches 1 from the left and to positive infinity as x approaches 1 from the right.
The complete question is here:
Which graph represents the function
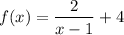 ?
?