Complete Question
The complete question is shown on the first uploaded image
Answer:
The answer is
 % higher than
% higher than

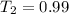 % lower than
% lower than

Step-by-step explanation:
From the question we are told that
The first string has a frequency of
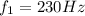
The period of the beat is

Generally the frequency of the beat is
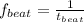
Substituting values
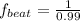
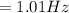
From the question
 for
for
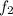 having a higher tension
having a higher tension
So
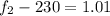

From the question
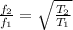
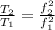
Substituting values
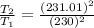
 % higher than
% higher than

For
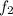 having a lower tension
having a lower tension
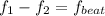
So
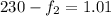

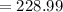
From the question
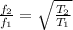
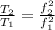
Substituting values
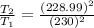
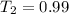 % lower than
% lower than
