Question

Suppose the horses in a large stable have a mean weight of 975lbs, and a standard deviation of 52lbs. What is the probability that the mean weight of the sample of horses would differ from the population mean by less than 15lbs if 31 horses are sampled at random from the stable? Round your answer to four decimal places.

Answer 1

0.8926 = 89.26% probability that the mean weight of the sample of horses would differ from the population mean by less than 15lbs if 31 horses are sampled at random from the stable

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

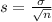For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this problem, we have that:

`\mu = 975, \sigma = 52, n = 31, s = (52)/(√(31)) = 9.34`

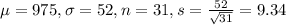
What is the probability that the mean weight of the sample of horses would differ from the population mean by less than 15lbs if 31 horses are sampled at random from the stable?

pvalue of Z when X = 975 + 15 = 990 subtracted by the pvalue of Z when X = 975 - 15 = 960. So

X = 990

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (990 - 975)/(9.34)`

`Z = 1.61`

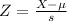
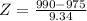
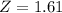
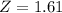`Z = 1.61` has a pvalue of 0.9463

X = 960

`Z = (X - \mu)/(s)`

`Z = (960 - 975)/(9.34)`

`Z = -1.61`

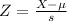
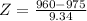
`Z = -1.61` has a pvalue of 0.0537

0.9463 - 0.0537 = 0.8926

0.8926 = 89.26% probability that the mean weight of the sample of horses would differ from the population mean by less than 15lbs if 31 horses are sampled at random from the stable