Question

A 10.5- resistor, a 15.9-μF capacitor, and a 15.2-mH inductor are connected in series with a 203-V generator. (a) At what frequency is the current a maximum? (b) What is the maximum value of the rms current? Note: The ac current and voltage are rms values and power is an average value unless indicated otherwise.

Answer 1

(a) Frequency at which current is maximum is 323.9 Hz

(B) Maximum current in the circuit is 19.333 A

Step-by-step explanation:

We have given resistance R = 10.5 ohm

Capacitance
`C=15.9\mu F=15.9* 10^(-6)F`

Inductance
`L=15.2mH=15.2* 10^(-3)H`

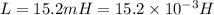
(a) Current is maximum when impedance will be minimum and impedance is minimum when there is condition of resonance.

At resonance
`X_C=X_L`

`(1)/(\omega C)=\omega L`

`\omega ^2=(1)/(15.9* 10^(-6)* 15.2* 10^(-3))`

`\omega =2034.13`

`2\pi f =2034.13`

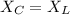
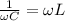
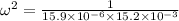
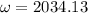
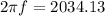
f = 323.9 Hz

(b) Current will maximum when resonance occurs at resonance impedance of the circuit is equal to resistance.

Voltage is given V = 203 volt

So maximum current
`i=(203)/(10.5)=19.333A`