Question

(1) Assume, you will receive rent payments over a time period of 44 years. For the first 22 years, you will receive a rent of $222 at the beginning of each year. For the next 22 years thereafter, you will receive $222 at the end of each year. (a) Employing the equation for identical payments over a limited time period, show how you would alter this equation applied to this problem. (b) Assuming a discount rate of 2% calculate the net present value of this income stream

Answer 1

• PW = $222 + $222(P/A, 2%, 44) - $222(P/F, 2%, 22)
• $6534

Step-by-step explanation:

Note : Rent received at the end of the year is equal to rent received at the beginning of a new year

1st payment received at the beginning of the 44 years period is termed payment received at year 0 = $222

so for the payments received at the end of year 1 in the second part of payment it is equivalent to rent received at the start of year 2 in the first part of payments and this through until the 21st year.

Identical payments are also received from year 23 to year 44 based on previous assumptions made BUT THERE IS NO IDENTICAL PAYMENT IN YEAR 22

A) applying equation for identical payments ( altered equation )

PW = $222 + $222(P/A, 2%, 44) - $222(P/F, 2%, 22)

PW of cash flow = identical cash flow per year + identical cash flow per year ( P/A, 2% , 44 ) - identical cash flow per year (P/F , 2% , 22 )

B) The net present value of the income system

(P/A ,2% ,44) =
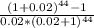`((1+0.02)^(44) - 1)/(0.02*(0.02 + 1)^(44) )` = 29.080

( P/F , 2%,22 ) =
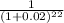`(1)/((1 +0.02)^(22) )` = 0.6468

back to the alerted equation

PW = $222 + $222* 29.080 - $222( 0.6468 )

= $6534

Answer 2

Ans: $6,534

Step-by-step explanation:

The given payment cash flows are described as follows:

1st payment in the year 0 = $222

Uniform annual payments of $222 are received at the end of years 1(is the same as the start of year 2) though 21

Uniform annual payments of $222 are received at the end of years 23 through 44.

The only missing payment in the uniform annual series is at the end of year 22.

a) PW of the given cash flow = $222 + $222(P/A, 2%, 44) - $222(P/F, 2%, 22)

b) (P/A, 2%, 44) = [(1+0.02)^44 - 1]/[0.02*(0.02+1)^44] = 29.080

(P/F, 2%, 22) = 1/(1+0.02)^22 = 1/1.02^22 = 0.6468

PW = $222 + $222*29.080 - $222*0.6468 = $6,534

Ans: $6,534