Answer:
Fraction of the specimen's is 0.4.
Step-by-step explanation:
We know,
Mass = volume × density
Weigh= mass × g
= volume × density× g
= density× g × volume
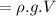
An object weighs less submerged due to buoyant force acting on it.
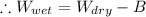
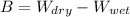
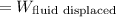

Given that, the weighs of the specimen in dry is twice of the weighs in air.

Then ,
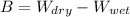
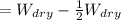

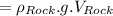
Therefore,
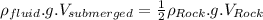
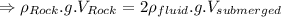
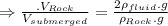
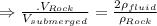
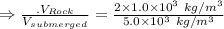
=0.4
Fraction of the specimen's is 0.4.