Question

In a population of 10,000, there are 5000 nonsmokers, 2500 smokers of one pack or less per day, and 2500 smokers of more than one pack per day. During any month, there is an 8% probability that a nonsmoker will begin smoking a pack or less per day, and a 2% probability that a nonsmoker will begin smoking more than a pack per day. For smokers who smoke a pack or less per day, there is a 10% probability of quitting and a 10% probability of increasing to more than a pack per day. For smokers who smoke more than a pack per day, there is an 8% probability of quitting and a 10% probability of dropping to a pack or less per day. How many people will be in each group in 1 month, in 2 months, and in 1 year? (Round your answers to the nearest whole number.)

Answer 1

In one month, we will have 4,950 non-smokers, 2,650 smokers of one pack and 2,400 smokers of more than one pack.

In two months, we will have 4,912 non-smokers, 2,756 smokers of one pack and 2,332 smokers of more than one pack.

In a year, we will have 4,793 non-smokers, 3,005 smokers of one pack and 2,202 smokers of more than one pack.

Explanation:

We have to write the transition matrix M for the population.

We have three states (nonsmokers, smokers of one pack and smokers of more than one pack), so we will have a 3x3 transition matrix.

We can write the transition matrix, in which the rows are the actual state and the columns are the future state.

- There is an 8% probability that a nonsmoker will begin smoking a pack or less per day, and a 2% probability that a nonsmoker will begin smoking more than a pack per day. Then, the probability of staying in the same state is 90%.

- For smokers who smoke a pack or less per day, there is a 10% probability of quitting and a 10% probability of increasing to more than a pack per day. Then, the probability of staying in the same state is 80%.

- For smokers who smoke more than a pack per day, there is an 8% probability of quitting and a 10% probability of dropping to a pack or less per day. Then, the probability of staying in the same state is 82%.

The transition matrix becomes:

`\begin{vmatrix} &NS&P1&PM\\NS& 0.90&0.08&0.02 \\ P1&0.10&0.80 &0.10 \\ PM& 0.08 &0.10&0.82 \end{vmatrix}`

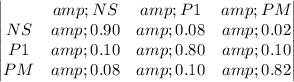
The actual state matrix is

`\left[\begin{array}{ccc}5,000&2,500&2,500\end{array}\right]`

We can calculate the next month state by multupling the actual state matrix and the transition matrix:

In one month, we will have 4,950 non-smokers, 2,650 smokers of one pack and 2,400 smokers of more than one pack.

To calculate the the state for the second month, we us the state of the first of the month and multiply it one time by the transition matrix:

In two months, we will have 4,912 non-smokers, 2,756 smokers of one pack and 2,332 smokers of more than one pack.

If we repeat this multiplication 12 times from the actual state (or 10 times from the two-months state), we will get the state a year from now:

In a year, we will have 4,793 non-smokers, 3,005 smokers of one pack and 2,202 smokers of more than one pack.