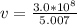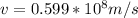Question

Light traveling from water to a gemstone strikes the surface at an angle of 80.0º and has an angle of refraction of 15.2º . (a) What is the speed of light in the gemstone? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

Answer 1

a

The the speed of light in the gemstone is
`v= 0.599*10^8 m/s`

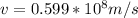
b

The unreasonable thing about this is that the speed of ligth in the gemstone is too low

the speed is 19% of the speed of light which is very low

c

One main unreasonable or inconsistent factor is that the assumption that the differnce between the angle of incidence and angle of refraction is very large

Step-by-step explanation:

From the question we are told that

The angle of incidence
`i = 80^o`

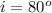
The angle of refraction
`r = 15.2^o`

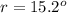
From Snell's law we have ,

`n_1 sin \theta_1 = n_2 sin \theta_2`

Where
`n_1` is the refractive index of the first medium (water) with a constant value of
`n_1 = 1..333`

`n_2` is the refractive index of the second medium (gem stone)

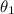`\theta_1` is the angle between the beam and perpendicular surface of the first medium

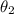`\theta_2` is the angle between the beam an the perpendicular surface of the second medium

Making the
`n_2` the subject of the formula

`n_2 = n_1 (sin \theta_1)/(sin \theta_2)`

`= (1.333)((sin (80.0))/(sin 15.2) )`

`= 5.007`

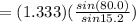
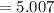
Generally refractive index of a material is mathematically represented

`n = (c)/(v)`

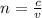
Where c is the speed light

v is the speed of light observed in a medium

Making v the subject

`v = (c)/(n)`

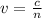
substituting value for gem stone

`v = (3.0*10^8)/(5.007)`

`v= 0.599*10^8 m/s`