Question

​Think about the proportion of students at your college who are wearing clothing that displays the college name or logo today. Also suppose that a friend of yours attends a different college, and the two of you have a recurring discussion about which college displays more school pride. You decide to measure school pride by the proportion of students at the college who wear clothing that displays the college name or logo on a particular day. You want to investigate whether this proportion differs between your college (call it Exemplary Students University, ESU) and your friend’s college (call it Mediocre Students University, MSU).

Suppose that you find that 24% of a random sample of students at ESU wears clothing with the school name or logo, compared to 16% of a random sample of students at MSU. Our research question: Is the observed difference in percentage of students wearing school clothing at ESU versus MSU statistically significant?

1. Which of the following is the appropriate null hypothesis?

In general, the percentage of ESU students who wear school clothing is the same as that of MSU students.

In general, the percentage of ESU students who wear school clothing is different from that of MSU students.

In general, a smaller percentage of ESU students wear school clothing compared to MSU students.

In general, a greater percentage of ESU students wear school clothing compared to MSU students.

2. Which of the following is the appropriate alternative hypothesis?

In general, a smaller percentage of ESU students wear school clothing compared to MSU students.

In general, the percentage of ESU students who wear school clothing is the same as that of MSU students.

In general, the percentage of ESU students who wear school clothing is different from that of MSU students.

In general, a greater percentage of ESU students wear school clothing compared to MSU students.

3. Calculate an appropriate statistic value to compare ESU students to MSU students with regard to wearing school clothing.

4. What additional information do you need in order to assess whether this difference calculated in part (c) is statistically significant?

Difference in population sizes between the two schools.

Sample size in each group

Population size of all ESU and MSU students

Proportion of students in each group

5. Describe a scenario, involving the additional information you cited in part (d), in which you believe that this difference would be statistically significant.

large

small

6. Describe a scenario, involving the additional information you cited in part (d), in which you believe that this difference would be NOT statistically significant. Choose the answer from the menu in accordance to the question statement

small

large

Answer 1

1. In general, the percentage of ESU students who wear school clothing is the same as that of MSU students.

2. In general, the percentage of ESU students who wear school clothing is different from that of MSU students.

3. Difference between proportions = 0.08

4. Sample size in each group

5. Large

6. Small

Explanation:

1. The null hypothesis usually express that there is no difference between certain characteristics of the populations.

In this case it would state that the proportions are the same for ESU and MSU.

The appropiate null hypothesis is:

In general, the percentage of ESU students who wear school clothing is the same as that of MSU students.

2. The alternative hypothesis express the claim that we are trying to test. In this case, that the proportion differs between ESU and MSU.

The appropiate alternative hypothesis is:

In general, the percentage of ESU students who wear school clothing is different from that of MSU students.

3. The only statistic that can be calculated is the difference between proportions:

`p_1-p_2=0.24-0.16=0.08`

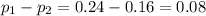
4. We need the sample size of each of both samples (ESU and MSU) in order to calculate the standard error.

Sample size in each group

5. The statistic z is calculated as the division of the difference of proportions, that will remain constant independent of the sample size, and the standard error, that depends on the sample size.

The standard error decreases with an increasing sample size. If the standard error decreases, the z-statistic increases, leading to a most extreme value that will eventually be statistically significant.

Then, a sufficiently large sample will lead to a difference that is statistically significant.

The right answer is:

large

6. Applying the same analysis as in point 5, only if the sample is small, the different would be not statistically significant.

The right answer is:

small