Answer:
a) 0.15rad/s
b) 0.26m/s
Step-by-step explanation:
a) To find the angular speed it is necessary to consider the conservation of energy. after the rock is dropped by the girl, the kinetic energy of the rock must equal the rotational energy of the merry-go-round joint the girl. In other words you have
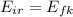
rotational energy and kinetic energy will given by:
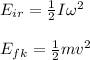
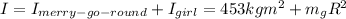
I: rotational inertia
w = angular speed
m: mass of the block
m_g: mass of the girl
R: radius of the merry-go-round
By replacing you have:
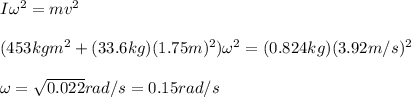
the angular speed is 0.15rad/s
b) the linear speed is given by:
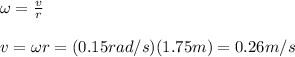
hence, the linear speed of the girl is 0.26m/s