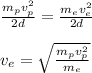Question

A proton of mass mp is released from rest just above the lower plate and reaches the top plate with speed vp. An electron of mass me is released from rest just below the upper plate. Calculate the speed ve of the electron when it reaches the bottom plate, in terms of vp, mp, me, and physical constants, as appropriate. Ignore gravitational effects.

Answer 1

`v_e=\sqrt{(m_pv_p^2)/(m_e)}`

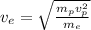
Step-by-step explanation:

You can consider that the force that acts over the proton is the same to the force over the electron. This is because the electric force is given by:

`F=qE`

`F_p=F_e`

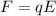
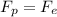
where E is the constant electric field between the parallel plates, and is the same for both electron and proton. Also, the charge is the same.

by using the Newton second law for the proton, and by using kinematic equation for the calculation of the acceleration you can obtain:

`m_pa_p=qE\\\\a_p=(v_p^2)/(2d)\\\\(m_pv_p^2)/(2d)=qE`

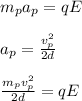
(it has been used that vp^2 = v_o^2+2ad) where d is the separation of the plates, ap the acceleration of the proton, vp its velocity and mp its mass.

By doing the same for the electron you obtain:

`(m_ev_e^2)/(2d)=qE`

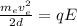
we can equals these expressions for both proton and electron, because the forces qE are the same:

`(m_pv_p^2)/(2d)=(m_ev_e^2)/(2d)\\\\v_e=\sqrt{(m_pv_p^2)/(m_e)}`