Answer:
c) P(270≤x≤280)=0.572
d) P(x=280)=0.091
Explanation:
The population of bearings have a proportion p=0.90 of satisfactory thickness.
The shipments will be treated as random samples, of size n=500, taken out of the population of bearings.
As the sample size is big, we will model the amount of satisfactory bearings per shipment as a normally distributed variable (if the sample was small, a binomial distirbution would be more precise and appropiate).
The mean of this distribution will be:
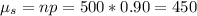
The standard deviation will be:
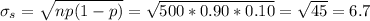
We can calculate the probability that a shipment is acceptable (at least 440 bearings meet the specification) calculating the z-score for X=440 and then the probability of this z-score:
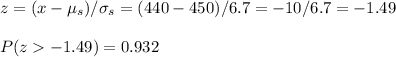
Now, we have to create a new sampling distribution for the shipments. The size is n=300 and p=0.932.
The mean of this sampling distribution is:

The standard deviation will be:
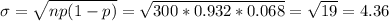
c) The probability that between 270 and 280 out of 300 shipments are acceptable can be calculated with the z-score and using the continuity factor, as this is modeled as a continuos variable:

d) The probability that 280 out of 300 shipments are acceptable can be calculated using again the continuity factor correction:
