Given:
Given that the measure of ∠A is 74°
The length of side b is b = 6.
The length of side c is c = 5.
The length of side BC is a.
We need to determine the value of BC.
Value of BC:
The value of BC can be determined using the law of cosine formula.
Thus, we have;
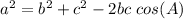
Substituting b = 6, c = 5 and ∠A = 74°, we get;
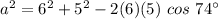
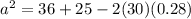


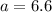
Thus, the length of BC is 6.6 units.