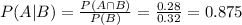Question

Among users of automated teller machines (ATMs), 92% use ATMs to withdraw cash, and 32% use them to check their account balance. Suppose that 96% use ATMs to either withdraw cash or check their account balance (or both). Given a woman who uses an ATM to check her account balance, what is the probability that she also uses an ATM to get cash?

Answer 1

0.875

Explanation:

Definition

The conditional Probability of an event A given that event B has occurred is:

`P(A|B)=(P(A\cap B))/(P(B)) , P(B)\\eq 0`

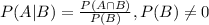
Let A=Event of Withdrawing Cash.

B=Event of Checking Account Balance.

We want to determine the probability that given a woman checks her account balance, she also gets cash. i.e. P(A|B)

`P(A)=0.92, P(B)=0.32, P(A\cup B)=0.96\\P(A\cup B)=P(A)+P(B)-P(A\cap B)\\0.96=0.92+0.32-P(A\cap B)\\P(A\cap B)=0.92+0.32-0.96=0.28`

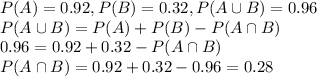
Therefore:

`P(A|B)=(P(A\cap B))/(P(B))=(0.28)/(0.32) =0.875`