Answer:
(1.2, 1.6)
Explanation:
Rewrite both equations to make y the subject:
Equation 1: 3x - y = 2
⇒ 3x = 2 + y
⇒ y = 3x - 2
This line has a positive slope.
Equation 2: 2x + y = 4
⇒ y = -2x + 4
This line has a negative slope.
Therefore, the graph that has been plotted is y = 3x - 2
Plotting second graph
Equation of the line: y = -2x + 4
Input x = 0 into the equation and solve to find the y-intercept:
⇒ y = -2(0) + 4 = 4
Therefore, the y-intercept is (0, 4)
Input y = 0 into the equation and solve to find the x-intercept:
⇒ 0 = -2x + 4
⇒ 2x = 4
⇒ x = 2
Therefore, the x-intercept is (2, 0)
Plot the two points (0, 4) and (2, 0), and draw a straight line that passes through them.
The solution to the system is the point of intersection of the two lines. From inspection of the graph, this is (1.2, 1.6)
------------------------------------------------------------------------------------------------
Solving algebraically
Equation 1: 3x - y = 2
Equation 2: 2x + y = 4
Sum the equations to eliminate y:
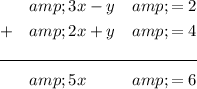
Solve for x:
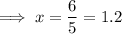
Substitute found value of x into one of the equations and solve for y:
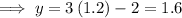
So the solution (point of intersection) of the system of equations is:
(1.2, 1.6)