Question

Big babies: The National Health Statistics Reports described a study in which a sample of 354 one-year-old baby boys were weighed. Their mean weight was 25.8 pounds with standard deviation 5.3 pounds. A pediatrician claims that the mean weight of one-year-old boys is greater than 25 pounds. Do the data provide convincing evidence that the pediatrician's claim is true? Use the =α0.05 level of significance and the P-value method with the TI-84 Plus calculator.

Answer 1

Yes. The data provide enough evidence to support the claim that the mean weight of one-year-old boys is greater than 25 pounds.

P-value=P(t>2.84)=0.0024

Explanation:

Hypothesis test on the population mean.

The claim is that the mean weight of one-year-old boys is greater than 25 pounds.

Then, the null and alternative hypothesis are:

`H_0: \mu=25\\\\H_a:\mu>25`

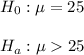
The significance level is α=0.05.

The sample size is n=354. The sample mean is 25.8 pounds and the sample standard deviation is 5.3 pounds. As the population standard deviation is estimated from the sample standard deviation, we will use a t-statistic.

The degrees of freedom are:

`df=n-1=354-1=353`

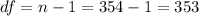
The t-statistic is:

`t=(\bar x-\mu)/(s/√(n))=(25.8-25)/(5.3/√(354))=(0.8)/(0.2817)=2.84`

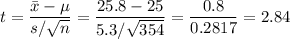
For a right tailed test and 353 degrees of freedom, the P-value is:

`P-value=P(t>2.84)=0.0024`

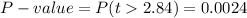
As the P-value is smaller than the significance level, the effect is significant and the null hypothesis is rejected.

There is enough evidence to support the claim that the mean weight of one-year-old boys is greater than 25 pounds.