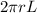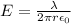Answer:
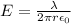
Step-by-step explanation:
We are given that
Linear charge density of wire=
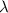
Radius of hollow cylinder=R
Net linear charge density of cylinder=
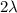
We have to find the expression for the magnitude of the electric field strength inside the cylinder r<R
By Gauss theorem
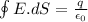
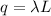
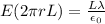
Where surface area of cylinder=