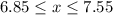Question

In order to estimate the mean 30-year fixed mortgage rate for a home loan in the United States, a random sample of 26 recent loans is taken. The average calculated from this sample is 7.20%. It can be assumed that 30-year fixed mortgage rates are normally distributed with a standard deviation of 0.7%. Compute 95% and 99% confidence intervals for the population mean 30-year fixed mortgage rate.

Answer 1

The 95% CI is (6.93% , 7.47%)

The 99% CI is (6.85% , 7.55%)

Explanation:

We have to estimate two confidence intervals (95% and 99%) for the population mean 30-year fixed mortgage rate.

We know that the population standard deviation is 0.7%.

The sample mean is 7.2%. The sample size is n=26.

The z-score for a 95% CI is z=1.96 and for a 99% CI is z=2.58.

The margin of error for a 95% CI is

`E=z\cdot \sigma/√(n)=1.96*0.7/√(26)=1.372/5.099=0.27`

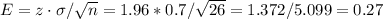
Then, the upper and lower bounds are:

`LL=\bar x-z\cdot\sigma/√(n)=7.2-0.27=6.93\\\\ UL=\bar x+z\cdot\sigma/√(n) =7.2+0.27=7.47`

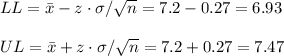
Then, the 95% CI is

`6.93\leq x\leq 7.47`

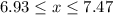
The margin of error for a 99% CI is

`E=z\cdot \sigma/√(n)=2.58*0.7/√(26)=1.806/5.099=0.35`

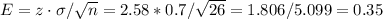
Then, the upper and lower bounds are:

`LL=\bar x-z\cdot\sigma/√(n)=7.2-0.35=6.85\\\\ UL=\bar x+z\cdot\sigma/√(n) =7.2+0.35=7.55`

Then, the 99% CI is

`6.85\leq x\leq 7.55`