Question

The time it takes students to complete a statistics quiz has a mean of 20.5 minutes and a standard deviation of 15.4 minutes. What is the probability that a random sample of 40 students will have a mean completing time greater than 25 minutes

Answer 1

"The probability that a random sample of 40 students will have a mean completing time greater than 25 minutes" is
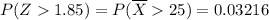`\\ P(Z>1.85) = P(\overline{X}>25) = 0.03216` or about 3.216%.

Explanation:

We have data normally distributed from which we are obtaining samples. Roughly speaking, for each of the possible samples we calculate its mean, and the result of all that is the distribution of the sample means.

The sampling distribution of the means behaves also like a normal distribution when the size of the sample is equal or greater than 30. When the data come from a normal distribution, the distribution of the sample means is always normal. Mathematically, we can say that

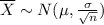`\\ \overline{X} \sim N(\mu, (\sigma)/(√(n)))` [1]

That is, the mean of this distribution is normal with mean
`\\ \mu` and standard deviation
`\\ (\sigma)/(√(n))`.

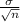And we also know that the random variable Z follows a standard normal distribution (this distribution has a mean = 0 and standard deviation = 1):

`\\ Z \sim N(0, 1)`

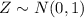
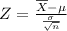`\\ Z = \frac{\overline{X} - \mu}{(\sigma)/(√(n))}` [2]

Where

`\overline{X}` is the mean of the sample. In this case,
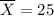`\overline{X} = 25` minutes.

The population mean is
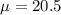`\\ \mu = 20.5` minutes.

The population standard deviation is
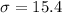`\\ \sigma = 15.4` minutes.

And, the sample size is
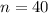`\\ n = 40` students.

With all this information at hand, we can continue as follows.

The probability that a random sample of 40 students will have a mean completing time greater than 25 minutes

Using the formula [2], we can determine the probability that the sample in question will have a completing time greater than 25 minutes. We can say that the random variable Z is like a standardized variable which behaves like a normal distribution, but with different mean and standard deviations (as described above, this distribution has mean = 0 and standard deviation = 1).

Therefore

`\\ Z = \frac{\overline{X} - \mu}{(\sigma)/(√(n))}`

`\\ Z = (25 - 20.5)/((15.4)/(√(40)))`

`\\ Z = (4.5)/(2.435)`

`\\ Z = 1.848 \approx 1.85`

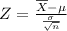
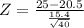
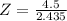
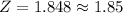
We can consult the cumulative standard normal table (available in any Statistics book or on the Internet) for
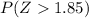`\\ P(Z>1.85)`. But, this table gives us values for
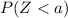`\\ P(Z<a)`. Then, we can find the corresponding complement probability as follows:

`\\ P(Z<1.85) = 1 - P(Z>1.85)`

Therefore

`\\ P(Z>1.85) = 1 - P(Z<1.85)`

`\\ P(Z>1.85) = 1 - 0.96784`

`\\ P(Z>1.85) = 0.03216`

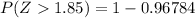
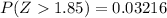
That is, "The probability that a random sample of 40 students will have a mean completing time greater than 25 minutes" is
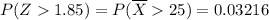`\\ P(Z>1.85) = P(\overline{X}>25) = 0.03216` or about 3.216%.

The graph below shows a standard normal distribution with the area that represents P(Z>1.85) = 0.03216.

The next graph the same probability for
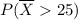`\\ P(\overline{X}>25)` minutes, with mean and standard deviation as described in [1].