Question

It is proposed to use Liquid Petroleum Gas (LPG) to fuel spark-ignition engines. A typical sample of the fuel on a volume basis consists of: 70% propane C3H8; 5% butane C4H10; and 25% propene C3H6 The higher heating values of the fuels are 50.38 MJ/kg for propane, 49.56 MJ/kg for butane, and 48.95 MJ/kg for propene. a) Work out the overall combustion reaction for stoichiometric combustion of 1 mole of LPG with air, and determine the stoichiometric F/A and A/F ratios. b) What are the higher and lower heating values per unit mass of LPG?

Answer 1

a)

The overall balanced combustion reaction is written as :

`0.7C_3H_8 \ + \ 0.05C_4H_(10) \ + \ 0.25 C_3H_6 \ + \ x(O_2 \ + \ 3.76N_2) ---> 3.05CO_2 \ + \ 3.8H_2O \ + \ 18.612N_2`

`(F/A)_(stoichiometric) = 0.0424`

`(A/F)_(stoichiometric) = 23.562`

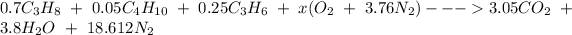
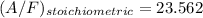
b)

the higher heating values
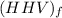`(HHV)_f` per unit mass of LPG = 49.9876 MJ/kg

the lower heating values
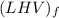`(LHV)_f` per unit mass of LPG = 46.4933 MJ/kg

Step-by-step explanation:

a)

The stoichiometric equation can be expressed as :

`0.7C_3H_8 \ + \ 0.05C_4H_(10) \ + \ 0.25 C_3H_6 \ + \ x(O_2 \ + \ 3.76N_2) ---> aCO_2 \ + \ bH_2O \ + \ cN_2`

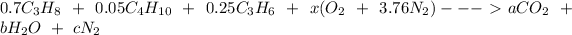
Now, equating the coefficient of carbon; we have:

(0.7×3)+(0.05×4)+(0.25×3) = a

a = 3.05

Also, Equating the coefficient of hydrogen : we have:

(0.7 × 8) +(0.05 × 10) + ( 0.25 × 6) = 2 b

2b = 7.6

b = 3.8

Equating the coefficient of oxygen

2x = 2a + b

`x = (2a+b)/(2) \\ \\ x = (2(3.05)+3.8)/(2) \\ \\ x = 4.95`

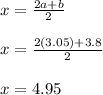
Equating the coefficient of Nitrogen

`c = 3.76x \\ \\ c = 3.76 *4.95 \\ \\ c = 18.612`

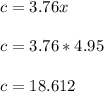
Therefore, The overall balanced combustion reaction can now be written as :

`0.7C_3H_8 \ + \ 0.05C_4H_(10) \ + \ 0.25 C_3H_6 \ + \ x(O_2 \ + \ 3.76N_2) ---> 3.05CO_2 \ + \ 3.8H_2O \ + \ 18.612N_2`

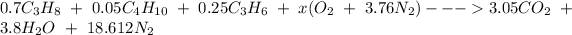
Now; To determine the stoichiometric F/A and A/F ratios; we have:

`(F/A)_(stoichiometric) = (n_f)/(n_a ) \\ \\ (F/A)_(stoichiometric) = (1)/(4.95*(1+3.76)) \\ \\ (F/A)_(stoichiometric) = 0.0424`

`(A/F)_(stoichiometric) = (n_a)/(n_f ) \\ \\ (A/F)_(stoichiometric) = (4.95*(1+3.76))/(1) \\ \\ (A/F)_(stoichiometric) = 23.562`

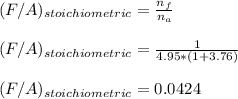
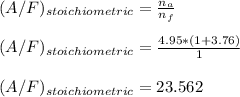
b)

What are the higher and lower heating values per unit mass of LPG?

Let calculate the molecular mass of the fuel in order to determine their mass fraction of the fuel components.

Molecular mass of the fuel
`M_f = (0.7*M_(C_3H_5) ) + (0.05 *M_{C_4H_(10)}) + (0.25*M _(C_3H_6))`

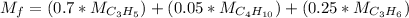
= 30.8 + 2.9 + 10.5

= 44.2 kg/mol

Mass fraction of the fuel components can now be calculated as :

`m_(C_3H_8) = (30.8)/(44.2) \\ \\ m_(C_3H_8) = 0.7 \\ \\ \\ m_{C_4H_(10)} = \frac[2.9}{44.2} \\ \\ m_{C_4H_(10)} = 0.06 \\ \\ \\ m_(C_3H_6) = (10.5)/(44.2) \\ \\ m_(C_3H_6) = 0.24`

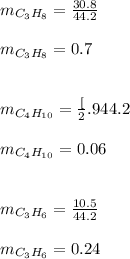
Finally; calculating the higher heating values
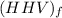`(HHV)_f` per unit mass of LPG; we have:

`(HHV)_f=(0.7 * HHV_(C_3H_8)) + (0.06 *HHV_{C_4H_(10)})+(0.24*HHV_(C_3H_6) \\ \\ (HHV)_f=(0.7*50.38)+(0.06*49.56)+(0.24*48.95) \\ \\ (HHV)_f=49.9876 \ MJ/kg`

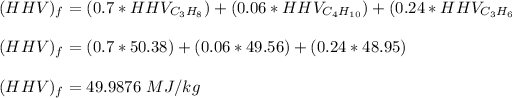
calculating the lower heating values
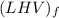`(LHV)_f` per unit mass of LPG; we have:

`(LHV)_f = (HHV)_f - \delta H_w \\ \\ (LHV)_f = (HHV)_f - [(m_w)/(m_f)h_(vap)] \\ \\ (LHV)_f = 49.9876 \ MJ/kg - [(3.8*18)/(44.2)*2.258 \ MJ/kg] \\ \\ (LHV)_f = 46.4933 \ M/kg`