Question

Jolly Blue Giant Health Insurance (JBGHI) is concerned about rising lab test costs and would like to know what proportion of the positive lab tests for prostate cancer are actually proven correct through subsequent biopsy. JBGHI demands a sample large enough to ensure an error of ±2 percent with 90 percent confidence. What is the necessary sample size?

Answer 1

Hence, the minimum required sample size (n) should be = 1692

Explanation:

Solution:-

- The estimation error, E = 2%

- The confidence level, CI = 90 %

- Since the proportion of the positive lab tests for prostate cancer are actually proven correct through subsequent biopsy are unknown we will assume the corresponding proportion to be p = 0.58

- The required sample size is a function of confidence value and error of estimation (E):

`n = p*( 1 - p ) * ((Z-critical)/(E))^2`

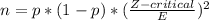
Where,

- The critical value of the confidence level = 90% would be:

significance level ( α ) = 1 - CI = 1 - 0.90 = 0.1

Z-critical = Z_α/2 = Z_0.05 = 1.645

- The required sample size (n) can be calculated:

`n = 0.5*( 1 - 0.5 ) * ((1.645)/(0.02))^2\\\\n = 1691.265`

- Hence, the minimum required sample size (n) should be = 1692