Question

For 40 days in the summer, you are working in a small, student-run company that sends out merchandise with university branding to alumni around the world. Every day, you take a sample of 50 shipments that are ready to be shipped to the alumni and inspect them for correctness. Across all days, the average percentage of incorrect shipments is 5 percent. What would be the center line for a p-chart?

Answer 1

The central line of the p-chart is 0.05.

Explanation:

In statistical quality control, the p-chart is a form of control chart used to observe the proportion of non-conforming or defective components in a random sample, where the sample proportion of defective items is defined as the fraction of the number of defective units to the size of the sample, n.

The central line of the p-chart is given by:

`CL=(\sum np)/(\sum n)`

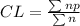
It is provided that:

The sample selected from a shipment for inspection every day is of size, n = 50.

The average percentage of incorrect shipments is 5%, i.e. p = 0.05.

Compute the number defective units in the sample as follows:

`np=50* (5)/(100)`

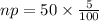
Compute the central line of the p-chart as follows:

`CL=(\sum np)/(\sum n)`

`=(5* 50)/(100* 50)\\`

`=0.05`

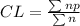
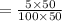
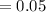
Thus, the central line of the p-chart is 0.05.