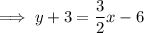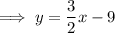Answer:

Explanation:
Equation of line m
If two lines are perpendicular to each other, the product of their slopes will be -1.
The slope of the line
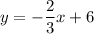 is
is

Therefore, the slope of the line m is:

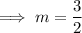
If line m passes through point (-2, -1), then the equation of line m is:
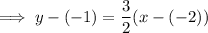

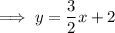
Equation of line n
If line n is parallel to line m, then they will have the same slope.
Therefore, slope of line n is
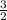
If line n passes through point (4, -3), then the equation of line n is: