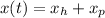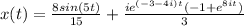Question

Consider the spring-mass-damper system defined by (all parameters are in SI units) 4� + 24� + 100� = 16���5� Assume zero initial conditions. Complete following steps. Part I a. Determine if the system is underdamped, critically damped or overdamped. b. Compute the steady-state response xp c. Compute the transient response xh d. Total response x(t) = xh + xp f. Plot x(t)

Answer 1

a) The system is under-damped

b) The steady state response,
`x_(p) = (8 sin(5t))/(15)`

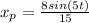
c) The transient response,
`x_(h) = (ie^((-3-4i)t)(-1+e^(8it) )/(3)`

d) The total response,
`x(t) = (8 sin(5t))/(15) +(ie^((-3-4i)t)(-1+e^(8it) ) )/(3)`

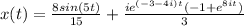
x(t) was plotted on matlab

Step-by-step explanation:

a) The equation is :
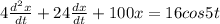`4(d^(2)x )/(dt) + 24(dx)/(dt) + 100x = 16 cos 5t`............(1)

The general equation of a spring-mass-damper system is given by:

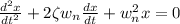`(d^(2) x)/(dt^(2) ) + 2 \zeta w_(n) (dx)/(dt) + w_(n) ^(2) x = 0`....................(2)

Comparing equation (1) with equation (2)

`w_(n) ^(2) = 100/4\\w_(n) = 52 \zeta w_(n) = 6\\2 * 5 * \zeta = 6\\\zeta = 0.6`

Since
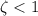`\zeta < 1`, the system is under-damped

b) Take the inverse laplace transform of equation (1)

`(4s^(2) + 24s + 100) X(s) = (16s)/(s^(2) + 25 )`

`(4s^(2) + 24s + 100)(s^(2) + 25) X(s) = 16s\\X(s) = (16s)/((4s^(2) + 24s + 100)(s^(2) + 25))`

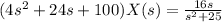
Taking the Inverse laplace transform of X(s)

`x(t) = (16 sin(5t))/(30) + 16 (ie^((-3-4i)t)(-1+e^(8it) )/(48)`

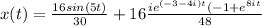
The steady state response is:

`x_(p) = (16 sin(5t))/(30)`

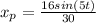
c) The transient response is:

`x_(h) = (16ie^((-3-4i)t)(-1+e^(8it) ) )/(48)\\x_(h) = (ie^((-3-4i)t)(-1+e^(8it) )/(3)`

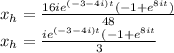
d) The total response:

`x(t) = x_(h) + x_(p) \\`

`x(t) = (8 sin(5t))/(15) +(ie^((-3-4i)t)(-1+e^(8it) ) )/(3)`