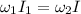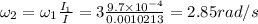Question

2. An object with moment of inertia ????1 = 9.7 x 10−4 kg ∙ m2 rotates at a speed of 3.0 rev/s. A 20 g mass with moment of inertia ????2 = 1.32 x 10−6 kg ∙ m2 is dropped onto the rotating object at a distance of 5.0 cm from the center of mass. What is the angular velocity of the combined object and mass after the drop?

Answer 1

2.85 rad/s

Step-by-step explanation:

5 cm = 0.05 m

20 g = 0.02 kg

When dropping the 2nd object at a distance of 0.05 m from the center of mass, its corrected moments of inertia is:

`I_2 = 1.32*10^(−6) + 0.02 * 0.05^2 = 0.513*10^(-4) kgm^2`

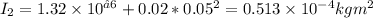
So the total moment of inertia of the system of 2 objects after the drop is:

`I = I_1 + I_2 = 9.7*10^(-4) + 0.513*10^(-4) = 0.0010213 kgm^2`

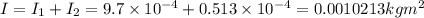
From here we can apply the law of angular momentum conservation to calculate the post angular speed

`\omega_1 I_1 = \omega_2 I`

`\omega_2 = \omega_1 (I_1)/(I) = 3 (9.7*10^(-4))/(0.0010213) = 2.85 rad/s`