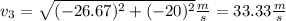Question

6. A frustrated physics student blew up her Physics textbook using a small amount of explosive. It broke into three pieces, which miraculously flew off in directions that were all in the same plane. A 0.200 kg piece flew off at 20.0 m/s and a 0.100 kg piece went off at 90° to the first piece, at 30.0 m/s. a) What was the momentum of the third piece? b) If the mass of the third piece was 0.150 kg, what was its velocity right after the explosion?

Answer 1

a) p₃ = 5 kg*m/s

b) v₃ = 33.33 m/s

Step-by-step explanation:

Given

m₁ = 0.200 kg

v₁ = 20.0 m/s i

m₂ = 0.100 kg

v₂ = 30.0 m/s j

m₃ = 0.150 kg

a) Using the equation p = m*v

p₃ = ?

If p₁ = m₁*v₁

and

p₂ = m₂*v₂

v = 0 m/s (speed of the the Physics textbook before the explosion)

m = mass of the Physics textbook before the explosion

We apply the following Principle

m*v = p₁ + p₂ + p₃

then

m*0 = m₁*v₁ + m₂*v₂ + p₃

⇒ 0 = (0.200 kg)*(20.0 m/s i) + (0.100 kg)*(30.0 m/s j) + p₃

⇒ 0 = 4 kg*m/s i + 3 kg*m/s j + p₃

⇒ p₃ = - 4 kg*m/s i - 3 kg*m/s j (i)

and its module is

`p_(3) =\sqrt{(-4)^(2) +(-3)^(2) } kg*(m)/(s) = 5 kg*(m)/(s)`

b) Using equation (i):

p₃ = - 4 kg*m/s i - 3 kg*m/s j

⇒ m₃*v₃ = - 4 kg*m/s i - 3 kg*m/s j

⇒ (0.150 kg)*v₃ = - 4 kg*m/s i - 3 kg*m/s j

⇒ v₃ = (- 4 kg*m/s/(0.150 kg)) i - (3 kg*m/s/(0.150 kg)) j

⇒ v₃ = - 26.67 m/s i - 20 m/s j

and its module is

`v_(3) =\sqrt{(- 26.67)^(2) +(- 20)^(2) } (m)/(s) = 33.33 (m)/(s)`