Question

asked Dec 2, 2021 73.0k views

1 Answer

Alextoind · Answer 1 · 2021-12-08T09:57:25+0000

Answer:

a) 54.68% probability that the next customer will arrive within the next 3 minutes

b) 15.78% probability that the next customer will arrive in more than 7 minutes

c) 56.27% probability that the next customer will arrive between 1 and 6 minutes

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

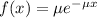
$f(x) = \mu e^(-\mu x)$

In which
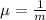$\mu = (1)/(m)$ is the decay parameter.

The probability that x is lower or equal to a is given by:

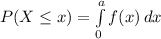
$P(X \leq x) = \int\limits^a_0 {f(x)} \, dx$

Which has the following solution:

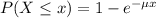
$P(X \leq x) = 1 - e^(-\mu x)$

During lunch hour, customers arrive at a fast food drive-through window, on average, every 3.8 minutes.

This means that
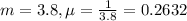
$m = 3.8, \mu = (1)/(3.8) = 0.2632$

a) What is the probability that the next customer will arrive within the next 3 minutes?

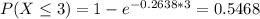
$P(X \leq 3) = 1 - e^(-0.2638*3) = 0.5468$

54.68% probability that the next customer will arrive within the next 3 minutes

b) What is the probability that the next customer will arrive in more than 7 minutes?

Either it will arrive in 7 minutes or less, or it will arrive in more than 7 minutes. The sum of the probabilities of these outcomes is decimal 1. So

$P(X \leq 7) + P(X > 7) = 1$

We want P(X > 7). So

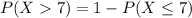
$P(X > 7) = 1 - P(X \leq 7)$

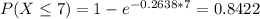
$P(X \leq 7) = 1 - e^(-0.2638*7) = 0.8422$

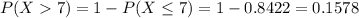
$P(X > 7) = 1 - P(X \leq 7) = 1 - 0.8422 = 0.1578$

15.78% probability that the next customer will arrive in more than 7 minutes

c) What is the probability that the next customer will arrive between 1 and 6 minutes?

$P(1 \leq X \leq 6) = P(X \leq 6) - P(X \leq 1)$

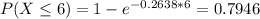
$P(X \leq 6) = 1 - e^(-0.2638*6) = 0.7946$

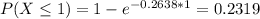
$P(X \leq 1) = 1 - e^(-0.2638*1) = 0.2319$

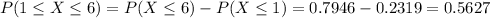
$P(1 \leq X \leq 6) = P(X \leq 6) - P(X \leq 1) = 0.7946 - 0.2319 = 0.5627$

56.27% probability that the next customer will arrive between 1 and 6 minutes

Please log in or register to add a comment.