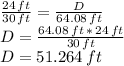Question

A perfectly straight 24 ft tall tree grows on the edge of the bank of a 45 foot wide river. A bird sitting at the top of the tree sees a fish in the middle of the river. At the same time as the fish begins to dive straight down, the bird flies in a straight line towards where it knows it will catch the fish. If the fish dives at a constant speed of 3 feet per second and the bird catches it in 2 seconds, how far from the top of the tree is the point where the bird meets the surface of the river

Answer 1

answer was 30 man

Explanation:

Answer 2

Distance covered by the bird before meeting the water is: 51.264 ft

Explanation:

Notice that if the bird catches the fish in 2 seconds, then the fish was able to dive down a total of 6 feet before being caught:

`distance=Vel\,* time=3\,(ft)/(s) *\,2\,\,s=6 \,\,ft`

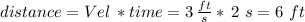
So the bird needs to fly in the direction of the hypotenuse of a right angle triangle (see attached image) that has one leg of length (24 ft + 6 ft) = 30 ft, and another one 22.5 ft (half the width of the river.

Such hypotenuse is (using Pythagoras theorem):

`hyp =√((60\,ft)^2+(22.5\.ft)^2) =√(4106.25) \,ft=64.08\,ft`

Now, in order to find the distance D the bird covers from the top of the tree to the water (marked in red in our image), we use similar triangles. The bigger triangle is that of legs 60 ft and 22.5 ft and hypotenuse 64.08 ft.

The smallest triangle we use in the proportion is the one shaded yellow in the image, which has one leg equal to 24 ft, and unknown hypotenuse:

So we make the proportion between known legs, and hypotenuses:

`(24\,ft)/(30\,ft) =(D)/(64.08\,ft) \\D=(64.08\,ft\,*\,24\,ft)/(30\,ft) \\D=51.264\,ft`