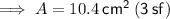Answer:

Explanation:

Sine Rule
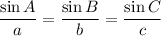
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
Cosine rule
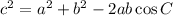
Area of a triangle
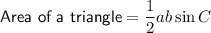
where:
- C is the angle
- c is the side opposite the angle
- a and b are the sides adjacent the angle

To find the area of ΔBCD, find:
- length of CD
- angle CDB
- length of BD
Then use the sine rule for area of a triangle
Calculate length CD using cosine rule:

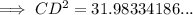
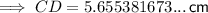
Calculate ∠ADC using sine rule:

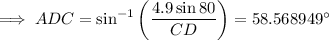
Therefore, ∠CDB = 180° - 58.568949° = 121.431051°
Use sine rule to calculate DB:
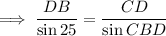
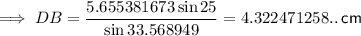

Use the sine rule for area of a triangle to find area of ΔBCD: