Question

1. What is the magnitude of the electric force of attraction between an iron nucleus (q = +26e) and its closest electron if the distance between them is 1.5*10-13 m? If you assume the electron is orbiting the nucleus (it doesn’t), determine how fast that electron is going. (0.27 N, 0.7c)

Answer 1

The magnitude of the electric force is 0.27N, and the speed of the electron is 211,000,000 m/s, about 0.7c.

Step-by-step explanation:

According to Coulomb's Law, we have that:

`F_e=(kq_1q_2)/(r^2)\\\\F_e=((9*10^9Nm^2/C^2)26(1.6*10^(-19)C)(1.6*10^(-19)C))/((1.5*10^(-13)m)^2)\\\\F_e=0.27N`

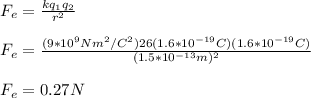
It means that the force of attraction between the nucleus and the electron is 0.27N.

Now, from the definition of centripetal force, we have:

`F_e=(m_ev^2)/(r)\\\\\implies v=\sqrt{(F_er)/(m_e)}`

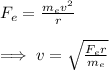
Considering that the mass of an electron is 9.1*10^-31 kg, and we know the magnitude of the electric force and the distance r, we can calculate the speed of the electron:

`v=\sqrt{((0.27N)(1.5*10^(-13)m))/(9.1*10^(-31)kg)}\\\\v=211,000,000m/s`

Having that the speed of light is about 3*10^8 m/s, then the speed of the electron is 0.7c.