Answer:
- Base Length = 7.368cm
- Height = 0.737cm.
Explanation:
Volume of the jewelry box=
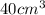
The box has a square base and is to be built with silver plated sides and nickel plated top and base.
Therefore: Volume = Square Base Area X Height = l²h

Total Surface Area of a Cuboid =2(lb+lh+bh)
Since we have a square base
Total Surface Area =
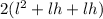
The Total Surface Area of the box
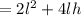
Nickel plating costs $1 per
Silver Plating costs $10 per
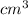
Since the sides are to be silver plated and the top and bottom nickel plated:
Therefore, Cost of the Material for the jewelry box
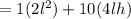
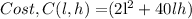
Recall earlier that we derived:

Substituting into the formula for the Total Cost

The minimum costs for the material occurs at the point where the derivative equals zero.
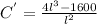
![4l^3-1600=0\\4l^3=1600\\l^3=400\\l=\sqrt[3]{400}=7.368 cm](https://img.qammunity.org/2021/formulas/mathematics/college/jd5zxxcxpjxzsr9a5rt8qxpmcp6tydpjov.png)
Recall:
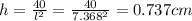
The box which minimizes the cost of materials has a square base of side length 7.368cm and a height of 0.737cm.