Question

You are given a solid that is a mixture of Na2SO4 and K2SO4. A 0.205-g sample of the mixture is dissolved in water. An excess of an aqueous solution of BaCl2 is added. The BaSO4 that is formed is filtered, dried, and weighed. Its mass is 0.298 g. What mass of SO4 22 ion is in the sample? What is the mass percent of SO4 22 ion in the sample? What are the percent compositions by mass of Na2SO4 and K2SO4 in the sample

Answer 1

To find the mass of SO4^2- ions in the sample, divide the mass of BaSO4 (0.298 g) by its molar mass. The mass percent of SO4^2- ions in the sample can be calculated by dividing the mass of SO4^2- ions by the mass of the sample mixture and multiplying by 100. The mass percent compositions of Na2SO4 and K2SO4 can be calculated in the same way.

Step-by-step explanation:

The first step in this problem is to calculate the number of moles of BaSO4 formed. We can do this by dividing the mass of BaSO4 (0.298 g) by its molar mass (233.43 g/mol). This gives us the number of moles of BaSO4.

Since the reaction between BaCl2 and Na2SO4 is a 1:1 stoichiometric ratio, the number of moles of BaSO4 formed is also the number of moles of SO42- ions present in the sample. To calculate the mass of SO42- ions, we multiply the number of moles by the molar mass of SO42- (96.06 g/mol).

The mass percent of SO42- ions in the sample is calculated by dividing the mass of SO42- ions by the mass of the sample mixture and multiplying by 100. The mass percent composition of Na2SO4 and K2SO4 can be calculated by dividing the mass of Na2SO4 or K2SO4 by the mass of the sample mixture and multiplying by 100.

Answer 2

Mass of SO₄⁻² = 0.123 g.

Mass percentage of SO₄⁻² = 41.2%

Mass of Na₂SO₄ = 0.0773 g

Mass of K₂SO₄ = 0.1277 g

Step-by-step explanation:

Here we have

We place Na₂SO₄ = X and

K₂SO₄ = Y

Therefore

X +Y = 0.205 .........(1)

Therefore since the BaSO₄ is formed from BaCl₂, Na₂SO₄ and K₂SO₄ we have

Amount of BaSO₄ from Na₂SO₄ is therefore;

`X*(Molar \, Mass \, of \, BaSO_4)/(Molar \, Mass \, of \, Na_2SO_4)`

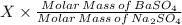
Amount of BaSO₄ from K₂SO₄ is;

`Y*(Molar \, Mass \, of \, BaSO_4)/(Molar \, Mass \, of \, K_2SO_4)`

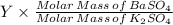
Molar mass of

BaSO₄ = 233.38 g/mol

Na₂SO₄ = 142.04 g/mol

K₂SO₄ = 174.259 g/mol

`X*(Molar \, Mass \, of \, BaSO_4)/(Molar \, Mass \, of \, Na_2SO_4)` =
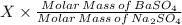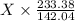`X*(233.38 )/(142.04)` = 1.643·X

`Y*(Molar \, Mass \, of \, BaSO_4)/(Molar \, Mass \, of \, K_2SO_4)` =
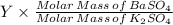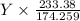`Y*(233.38 )/(174.259 )` = 1.339·Y

Therefore, we have

1.643·X + 1.339·Y = 0.298 g.....(2)

Solving equations (1) and (2) gives

The mass of SO₄⁻² in the sample is given by

Mass of sample = 0.298

Molar mass of BaSO₄ = 233.38 g/mol

Mass of Ba = 137.327 g/mol

∴ Mass of SO₄ = 233.38 g - 137.327 g = 96.05 g

Mass fraction of SO₄⁻² in BaSO₄ = 96.05 g/233.38 g = 0.412

Mass of SO₄⁻² in the sample is 0.412×0.298 = 0.123 g.

Percentage mass of SO₄⁻² = 41.2%

Solving equations (1) and (2) gives

X = 0.0773 g and Y = 0.1277 g.