Question

The International Space Station is orbiting at an altitude of about 370 km above the earth's surface. The mass of the earth is 5.976 × 1024 kg and the radius of the earth is 6.378 × 106 m. Assuming a circular orbit, what is the period of the International Space Station's orbit?

Answer 1

T = 5516.63 seconds

Step-by-step explanation:

Given that,

The International Space Station is orbiting at an altitude of about 370 km above the earth's surface.

Mass of the Earth,
`M=5.976 * 10^(24)\ kg`

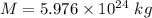
Radius of Earth,
`r=6.378* 10^6\ m`

We need to find the period of the International Space Station's orbit. It is a case of Kepler's third law. Its mathematical form is given by :

`T^2=(4\pi^2)/(GM)* R^3`

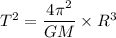
R = r + h

`T^2=(4\pi^2)/(6.67* 10^(-11)* 5.976 * 10^(24))* (370000+6.378* 10^6)^3\\\\T^2=30433264.1641\ s\\\\T=5516.63\ s`

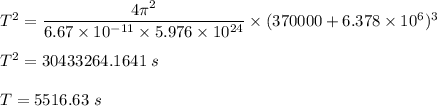
So, the period of the International Space Station's orbit is 5516.63 seconds.